Invers Matriks Menggunakan Metode Operasi Baris Elementer dan Partisi Matriks

NAMA : DEWI SARTIKA
NIM : 201831068
KELAS : B
GURU PEMBIMBING : EFY YOSRITA,S.SI.M.Kom
![\left[ \left.\begin{matrix} 1& 1& 2\\ 2& 4& -3\\ 3& 6& -5 \end{matrix}\right| \begin {array}{r} 9\\ 1\\ 0\end {array}\right] \left[ \left.\begin{matrix} 1& 1& 2\\ 2& 4& -3\\ 3& 6& -5 \end{matrix}\right| \begin {array}{r} 9\\ 1\\ 0\end {array}\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cleft.%5Cbegin%7Bmatrix%7D++1%26+1%26+2%5C%5C+2%26+4%26+-3%5C%5C+3%26+6%26+-5+%5Cend%7Bmatrix%7D%5Cright%7C+%5Cbegin+%7Barray%7D%7Br%7D+9%5C%5C+1%5C%5C+0%5Cend+%7Barray%7D%5Cright%5D&bg=ffffff&fg=666666&s=0)
Persamaan
diatas dapat dinyatakan dalam bentuk matriks dengan komponenya yaitu matriks
koefisien, matriks variabel dan matriks output sebagai berikut
OPERASI BILANGAN ELEMENTER :
Untuk
menentukan solusi dari SPL dilakukan dengan cara membentuk matrik yang
diperluas/diperbesar dari SPL dan melakukan Operasi Baris Elementer
(OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam
suatu tahapan dengan menerapkan ketiga tipe operasi berikut untuk
menghilangkan bilangan-bilangan tak diketahui secara sistematik.
-
Kalikan persamaan dengan konstanta yang tak sama dengan nol.
-
Pertukarkan dua persamaan tersebut.
-
Tambahkan kelipatan dari satu persamaan bagi yang lainnya.
Karena
baris (garis horisontal) dalam matriks yang diperbesar beresuaian
dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut,
maka ketiga operasi ini bersesuaian dengan operasi berikut pada baris
matriks yang diperbesar.
-
Kalikanlah sebuah baris dengan sebuah konstanta yang taksama dengan nol.
-
Pertukarkanlah dua baris tersebut.
-
Tambahkanlah perkalian dari satu baris pada baris yang lainnya.
Operasi-operasi ini dinamakan Operasi Baris Elementer (OBE).
Sifat-sifat matriks yang berbentuk eselon baris (row-echelon form) dan eselon baris tereduksi (reduced row-echelon form) :
-
Jika baris tidak terdiri seluruhnya dari nol, maka bilangan taknol pertama dalam baris tersebut adalah 1. (kita namakan ini 1 utama).
-
Jika terdapat baris yang seluruhnya terdiri dari nol, maka semua baris seperti itu dikelompokkan berama-sama dibawah matriks.
-
Dalam sebarang dua baris yang berurutan yang seluruhnya tidak terdiri dari nol, maka 1 utama dalam baris yang lebih rendah terdapat lebih jauh kekanan dari 1 utama dalam baris yang lebih tinggi.
-
Masing-masing kolom yang mengandung 1 utama mempunyai nol di tempat lain.
Dikatakan matriks berada dalam bentuk eselon baris jika memiliki sifat 1, 2, dan 3. Prosedur untuk mereduksi menjadi eselon baris tereduksi disebut Eliminasi Gauss-Jordan. Jika memiliki keempat sifat tersebut, maka matriks tersebut berada dalam bentuk eselon baris tereduksi dan prosedurnya disebut Eliminasi Gauss.
Contoh 1 :
Carilah solusi dari persamaan dibawah ini dengan menggunakan OBE.
x + y + 2z = 9
2x + 4y – 3z = 1
3x + 6y – 5z = 0
Penyelesaian :
Ubah persamaan tersebut kedalam bentuk matriks yang diperbesar
kemudian gunakan OBE :
- baris kedua : B2 + (-2)B1,
baris ketiga : B3 + (-3)B1,
- baris kedua : B2 x (1/2),
- baris ketiga : B3 + (-3)B2,
- baris ketiga : B3 x 2,
pada matriks terakhir ini dinamakan matriks berada dalam bentuk eselon baris. Dari matriks eselon baris ini dapat ditulis kedalam bentuk persamaan yang bersesuaian dengan matriks tersebut.
x + y + 2z = 9
y – 7/2 z = -17/2
z = 3
sehingga dengan mensubstitusikan z = 3 kedalam persamaan kedua, diperoleh y – 7/2(3) = -17/2  y = 2. Setelah itu substisikan z dan y kepersamaan pertama, diperoleh x + 2 + 2(3) = 9
y = 2. Setelah itu substisikan z dan y kepersamaan pertama, diperoleh x + 2 + 2(3) = 9  x = 1.
x = 1.
Jadi, solusi dari persamaan diatas adalah x = 1, y = 2 dan z = 3.
Kita
juga bisa mencari solusi persamaan tersebut dengan cara mengubah
matriks tersebut sampai dalam bentuk matriks eselon baris tereduksi,
hasil akhirnya akan sama. Misal matriks eselon baris tersebut kita ubah
kedalam eselon baris tereduksi.
- baris kedua : B2 + (-7/2)B3,
baris pertama : B1 + (-2B3),
- baris pertama : B1 – B2,
Dari matriks eselon baris tereduksi diatas diperoleh x = 1, y = 2 dan z = 3.
Pengertian Metode Partisi Matriks :
→ Metode Partisi Matriks adalah metode penyelesaian yang digunakan untuk menyederhanakan matriks yang ukurannya besar menjadi matriks kecil sehingga lebih mudah dioperasikan untuk tujuan tertentu.
Partisi
Matriks A yang berordo (m x n ) yang diperoleh dari A dengan cara
memberikan batasan-batasan garis horisontaldiantara dua baris dan atau
memberikan batasan-batasan garis vertikal diantara dua kolom.
Dari persamaan tersebut maka persamaan awal dapat dinyatakan dengan

Dengan hanya berbekal kemampuan menguasai invers matrix dengan dimensi 2x2, maka kita dapat
melakukan invers matriks yang berdimensi mxn dengan sangat mudah.
Motode partisi dapat
membantu perhitungan invers dari matriks-matriks yang berorder tinggi.
Matriks inversi A dinotasikan dengan A-1
yang merupakan pembagian adjoin matriks A dengan determinannya, seperti berikut
Dari persamaan tersebut, maka diketahui bahwa dimensi matriks
A sangat besar, maka perhitungan
adjoin dan determinannya menjadi sangat rumit. Oleh karena itu, perlu pemecahan
menggunakan metode partisi agar dimensi matriks menjadi lebih kecil.
Metode partisi adalah salah satu metode yang dapat
digunakan untuk menginverse matriks yang berdimensi besar. Sebuah matriks yang
akan dicari inversnya dipartisi menjadi 4 matriks sebagai berikut:
Syarat utama dari proses partisi adalah matriks A1 dan A4 harus bujur sangkar. Untuk memudahkan pengoperasian inversi dari matriks A yaitu A-1 dapat ditulis sebagai berikut:




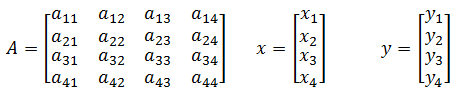

Komentar
Posting Komentar